当前位置：首页 » 深国交哲学社 » 正文

用游戏解释语言：博弈语义简介（上）

7461 人参与 2023年03月13日 20:10 分类 : 深国交哲学社评论

语言的意义[1] 是如何生成的？在语言学家和逻辑学家的传统观点中，基本语言片段的意义由词库指定，在一门语言中相对固定，幼儿通过学习这个词库来掌握意义，而复杂片段的意义则由其组成部分的意义决定. 这种观点下，意义不涉及主体的行为，可以称为「零主体的意义」. 而从上世纪七十年代开始，将意义视为信息交互的观点开始兴起：言说者通过语言改变听者头脑中的信息状态，而意义便由这种变化确定：一句话的意义就是其能给接受该句子的人带来的信息变化. 这种观点下，意义涉及言说者的目的与行为，因此可以称为「单主体的意义」. 兴盛于阿姆斯特丹的动态语义学 (dynamic semantics) 即以此为基础建立，传统的语义学-语用学的分野在这个框架下重新划定，自然语言在其中也被看作是用以改变主体状态的编程语言.

[1] 本文中不会严格区分意义和指称.

一旦将信息交互纳入考虑范围，我们自然可以更进一步：既然只有当一句话对听者引起了言说者所希望的信息改变时，交流才是成功的，而听者对这句话又可能有不同于言说者所希望的解读，因此可以想象，在语言互动的过程中，言说者在措词造句时，需要考虑听者会如何解读（「我需要知道你知道什么」），而听者在解读时也会相应地考虑到言说者会如何考虑自己如何解读（「我需要知道你知道我知道什么」），以此类推. 语言的意义，便隐伏在如此织就的信念、知识与信息之网中，这便是「双主体的意义」[2].

[2] 以上两段内容主要概括自van Benthem (2008).

可能这样的引入有些抽象，下面的两个例子或许能展现一些知识与语言意义交互的风味. 考虑以下情景：某次战役中，两个将领和分驻敌军阵地两侧，两人都知道各自的部队单独进攻都会被歼灭，只有同时进攻才能取胜. 由于无线电通讯被干扰，两人事先约定凌晨四点一起进攻. 即将发动进攻时，发现情况有变，于是派人往驻地报信：计划有变，听到任何人的枪响后一起进攻（这条消息简记为). 得知消息后心想：现在并不能确定我是否知道, 因此也不敢发起进攻. 于是也派人向回信. 得知消息后心想：现在并不能确定我是否知道知道了, 因此即使听到枪响也不敢发起进攻 [3]. 于是又派人向回信. 得知消息后心想：现在并不能确定我是否知道了知道了我知道了, 因此……如此下去，两人永远无法开始进攻 [4]. 在这里，由于信息交互的不完整，的枪响无法传递任何意义，即使所有人都能听到.

[3] 枪响可能是敌人发出的，因此不能认为B 能如下推理：「如果A不确定，A就不会开枪，因此只要有枪响，就说明A已经收到了回信」.

[4] 如果出于意外，有人开了枪，那么A, B 两方都会因为无法确定对方会进攻而逃跑，这种无法确定是出于对对方认知状态的了解（或不了解），而非不够信任对方.

考虑另一个情景 [5]：在一个英国小镇上，Johann是唯一的德国人. 一天他去喝啤酒，刚进酒吧门口，Martin便大声笑道：「Hans又来喝啤酒了！」众人皆笑. 镇上没有人叫Hans. 但这句话成功地传递了应有的意义，每个人都知道Hans这个名字说的是Johann. 这是如何做到的？正是由于Martin知道镇上没有人叫Hans，且每个人都知道Martin知道镇上没有人叫Hans，且Martin知道每个人都知道Martin知道镇上没有人叫Hans，且……因此，所有人都知道Martin必然另有所指，而最合适的对象便是Johann（为什么Johann最合适？因为Martin知道Hans是常见的德国男名而Johann是德国男人且常来喝啤酒且刚刚进酒吧，且每个人都知道Martin知道这些，且……）

[5] 该例子来源于唐浩老师两年前在清华大学讲授《近代西方哲学》的课程讲义.

可以看出，意义和语言群体中的信息交互、合作与公共知识有着密切的关系，而这些主题能够在博弈论中自然地表示. 因此，我们有了一种别于传统语义学的思路：用博弈确定意义. 这看似新奇，事实上在晚期维特根斯坦的语言游戏中便有朴素的呈现，甚至Peirce就已经提出过可以把量词解释为双人博弈了. 我们可以用不同方式将这一思路发展成型，在其中一种路线中 [6]，我们把每个句子都看作一场博弈，用虚拟玩家的必胜策略存在与否确定句子的真值. 本文即是对这种博弈语义 (game-theoretical semantics) 如何解释逻辑语言和自然语言意义的初步介绍. 因为这些讨论会不可避免地涉及形式逻辑等内容，而本文不预设读者具有任何相关知识（除了高中程度的集合论，如什么是（朴素定义的）集合，什么是等），因此在进入主要内容之前，本文会首先花一些篇幅，以尽可能易懂的方式介绍最基础的一阶逻辑语言. 了解这些内容的读者可以直接略过第一节.

[6] 本文第8节会讨论其他方式. （本文后半段于下期推送发出）

全文目录：

1 预备知识：一阶逻辑语言的语法与语义简介

2 语言游戏：另一种语义

3 一阶逻辑语言的博弈语义

4 IF-逻辑及其博弈语义

5 IF-逻辑和博弈语义的一些特点

5.1 表达力强于 FOL

5.2 并非非真即假

5.3 非组合性

6 自然语言的信息独立

6.1 量词独立

6.2 引入模态

6.3 否定移位

6.4 模态不透明：De re - de dicto 之别

6.5 现实算子与可能世界回退

7 自然语言的博弈语义

8 更多视角，更多博弈

预备知识：一阶逻辑语言的语法与语义简介

在研究语言时，我们把被研究的语言称为目标语言，把用来研究讨论目标语言的语言称为元语言. 在这篇文章中，元语言以汉语为主，夹杂一些形式化符号，对象语言在本文不同部分中则分别是逻辑语言和自然语言（汉语、英语等）. 本节中将时刻提醒读者注意这二者的区分.

逻辑语言多种多样，其中最基本的一类称为一阶逻辑 (first-order logic, 下文简称FOL), 又称谓词逻辑. 介绍FOL常见的做法是首先给出其完整的语法（也就是这门语言在形式上是怎样的，有哪些符号和句子），然后再定义其语义（也就是各个符号和句子都是什么意思）. 但本文为了便于读者理解，会将两部分夹杂着介绍. 本节中定义的语义是FOL的「标准」语义，我们称为Tarski语义 [7]. 如无特殊说明，本节下文中的「逻辑语言」均指FOL.

[7] Alfred Tarski是早期的逻辑学家，对这套语义有重要贡献.

FOL由以下几类符号构成 [8]：

[8] FOL并没有一个标准版本，这里只是我给出的一种定义. 同时，本文为方便和可读性起见，会使用 y, b 这样的不在下述列表内的非标准符号表示FOL.

(1) 常量符号：, , ...
(2) 变量符号：, , ...
(3) -元关系符号：, , ...
(4) 连结词：, ,
(5) 量词：,
(6) 等号：
(7) 辅助符号：,

这些符号所要表达的意思大都很直白，比如一个常量符号似乎就是要表达一个特定的对象，这个对象可以是字母，可以是某个特定的数, 可以是Tarski其人，仿佛世界上的所有东西都能被常量符号指代，毕竟这只是一个没有内容的符号嘛. 但问题没有这样简单. 能不能表达黑格尔所说的绝对精神？能不能表达某个特定的比0小的自然数？呃，这个问题的回答似乎取决于绝对精神和小于0的自然数到底是不是世界上存在的东西. 但为什么一定要把常量符号指代的范围限制在存在的东西呢？不存在之物是否也能被指代，就像「无色的绿色思想」一样？

事实上，说明指代范围至关重要，因为不同的指代范围会造成同一个语言片段不同的解释. 比如，当我们论及的范围囊括不存在之物时，「存在」这句话就不一定为真，否则则一定为真. 因此在解释常量符号的意义时，需要援引一个论域作为背景，所有常量符号都被解读成其中的一个个体，变量则可以在这个论域范围内取值. 自然地，我们用集合表示论域，在此基础上定义一个解释函数 [9]. 用来解释逻辑语言中的符号. 对于常量符号，我们有 . 变量符号不被解释，它和常量符号的性质不同. 如果说常量符号是名字（即专有名词），变量符号就是代词，解释函数的作用则相当于词典，把符号翻译成其所指代的东西. 代词he当然可以在具体语境中指代具体的人，但这不影响这个词在任何一部词典中都不会被解释成某个具体的人，而只会是个可以代指论域内任意个体的代词. 与此相反，名字在一部词典里一定会被解释成一个个体. 容易看出，同一个逻辑语言片段，不同的解释会影响其意义.

[9] 严格说来此处应该用映射一词，函数是数集到数集的映射. 本文不区分这两个术语.

没有接触过离散数学等学科的读者可能不太清楚什么是「关系」. 「……比……（数字上）大」就是一个关系，当两个空位上填上论域内的各种个体时这个关系可能成立也可能不成立，比如「比3大」成立，「Tarski比a大」不成立. 我们也可以说这个二元组满足这个关系，Tarski, a不满足. 这是一个二元关系，因为它涉及两个个体. -元关系涉及个个体. 我们可以用所有满足某关系的-元组（注意，这是元语言而非逻辑语言的表述！）的集合来表示一个-元关系，比如父子关系就可以表示为所有父子对 (pairs of father-son) 的集合. 这样的关系就是逻辑语言中的关系符号所要指代的对象，解释函数把后者翻译成前者：, 其中是论域（如所有人），是论域中的个体可能排列成的所有-元组的集合（如所有二人组，当时），其中只有一部分满足所代表的关系（如父子对）. 特别地，逻辑语言中的也是一个二元关系符号，但其意义不被解释函数决定，而是永远表示相等关系，可以表示成所有的集合，其中为论域中的任意个体. 这类表达也可以被写作，以便阅读.

[10] 应该说是二人有序组，因为这个组内的个体顺序是固定的，比如父子对和子父对就不一样，后者不满足父子关系.

至此，细心的读者也许已经发现，我们已经可以写出一些句子了. 比如，说的是和代表的个体构成的二元组满足代表的关系，即. 重要的是，这个FOL句子可以被判断真假，因为我们刚刚就已经将其完整地翻译成了元语言句子，那么只需要用我们对元语言的知识判断后者的真假就能得出前者的真假. 将这个真假定义一般化，得到：为真，当且仅当

成立. 这样，我们就定义了一类逻辑语言句子的真假.

事实上，既然变量符号也指代个体，那自然也可以占据关系中的位置，如. 但由于变量符号指代的个体是不固定的，所以这样的表达式和不一样，所表达的具体内容不固定，也没有确定的真值（即真-假取值），因此不能被称为句子. 为此，我们引入公式这个新的概念. 具有如下形式的字符串被称为一个原子公式：

注意，这是一个元语言记号，其中指逻辑语言中的任意一个-元关系符号（包括），指逻辑语言中的任意一个常量符号或变量符号.之所以称为原子公式，是因为这是逻辑语言中能用来表达内容的最简单的片段，不能再加以拆分.

我们可以在原子公式的基础上利用逻辑连结词和量词构造更复杂的公式：

定义1（FOL公式）：
(1) 形如的字符串是公式.
(2) 如果是公式，那么也是公式.
(3) 如果和都是公式，那么和也都是公式.
(4) 如果是公式，那么和也都是公式.

注意这里的表述都是元语言，逻辑语言里并没有这样的符号. 括号是用来避免歧义的，如果没有括号，这样的公式会出现歧义. 对这类不存在此类情况的句子，可以把括号删去.

至此，FOL的句法已被定义完毕. 我们通过真值定义解释这些连结词的意义：是「非」连结词，如果是个句子，的真值与相反. 是「且」连结词，如果和都是句子（下同），为真当且仅当和都为真. 是「或」连结词，为真当且仅当和至少有一个为真.

至于量词，是用来约束公式中的变量的. 粗略地说，即是「所有」，即是「存在」，如的意思就是「存在使得」，而这显然在给定的论域和解释下可以判断真假. 可以发现，本来并不是具有真值的句子，但当前面加上后，便成为了句子，这是因为其中的变量受到了量词的约束. 同一公式中的同一变量可能在此处受约束，在彼处不受约束，如中前两次出现不受约束，最后一次出现则受约束. 我们把一个公式中变量没有被约束的出现称为其自由出现，被量词约束的称为约束出现. 非句子的公式之所以不能表达具体的命题就是因为其中自由出现的变量所指代的对象不确定，因此当一个公式中没有自由出现的变量时，它便是一个句子.

在中 (为量词记号，可以是或), 将称为的辖域 (scope), 约束其辖域内的所有. 如果是公式，那么用表示将中所有自由出现的变量符号替换成常量符号所得到的公式，如对于上面的例子，假设在元语言中称其为，则表示下面这个逻辑语言中的公式：. 至此，我们可以解释量词的语义了：为真，当且仅当对于论域中的每一个个体，为真；为真，当且仅当对于论域中存在一个个体，使得为真.

以上，我们基本完整地描述了FOL的语法与语义，在此对其语义（即句子为真的条件）进行形式化整理，以作为本节的结尾. 首先，我们已经说明了，句子的真值是依赖于论域和解释的，将后两者统称为模型：，其中为模型，为论域，为解释函数，该函数把常量符号解释为论语中的个体，把关系符号解释为基于论域上的关系. 同一个句子在不同的模型中真值可能不一样，我们在元语言中用表示句子在模型中为真（或称模型满足句子），表示为假[11]. 我们有：

[11] 严格来说，是「句子在模型中非真」的意思. 但FOL的Tarski语义是非真即假的，所以我们可以称上述表达式表示「句子在模型中为假」.}

定义2（FOL 真句子）：
(1) ，当且仅当.
(2) ，当且仅当.
(3) ，当且仅当且.
(4) ，当且仅当与中至少一个成立.
(5) ，当且仅当对于任意，.
(6) ，当且仅当存在使得.

在每一条定义中，「当且仅当」左边的部分说的都是逻辑语言句子（尽管用元语言记号表示）为真，右边的部分都是用元语言表示的条件（如「」「且」等），也就是用元语言定义了逻辑语言句子为真的条件. 同时，由于左边的部分含有连结词或量词而右边没有，这些也可以看成对连结词和量词的定义.

用游戏解释语言：博弈语义简介（上）哲学第3张语言游戏：另一种语义

Tarski语义看起来很不错，既自然又简单. 为什么要再发明别的语义呢？我们将在后续部分说明Tarski语义在应用上的局限，但首先，本节会基于语言游戏这一概念简单说明其在哲学上的不足. 考虑下面两个问题：语言片段和其对应的现实世界是如何连接的？我们语言使用者又是如何确定语言表述的含义？早期维特根斯坦用图像论回答了前者，Tarski语义则回答了后者. 在此先为对图像论不甚熟悉的读者略作介绍.

Stenius (1960) 将图像论表述为「世界的成分被与其逻辑类型相同的语言实体表示」 (the ingredients of the world are represented in the language by entities of the same logical type). 注意这里的「语言实体」不是「语言符号」，而是「个体」、「元关系」这样的对象. 在此我们需要区分 [12] 三个不同的概念：世界中的关系（所有满足条件的-元组的集合）、语言中的关系、语言中用来表示关系的符号. 前二者的区别在于一个以世界中存在的实体为论元，一个以语言片段为论元，而它们都可以被语言中的符号表示. 如假设是逻辑语言中的一个二元关系符号，成立当且仅当代表的实体和代表的实体满足代表的关系，那么便定义了一个世界中的二元关系. 但同时也定义了一个语言中的关系，它的论元是「」「」这样的逻辑语言中的变元. 维特根斯坦的图像论说的是，（语言中的关系）表示（现实中的关系），并且二者逻辑类型相同. 而Tarski语义说的则是，（语言符号）表示（现实中的关系）.

[12] 这个区分来自 Hintikka (1977).

Hintikka (1977) 指出，图像论和Tarski语义非常相似. 首先，根据两个理论得出的语言中的句子为真的条件完全相同，这可以从上面的例子中看出. 更重要的是，两种理论都把语言和其对应的世界之间的表示关系当作一种基本概念，不再进一步分析（用导言第一段的说法，它们都是「零主体的意义」），它在《逻辑哲学论》中被称为命名，在Tarski语义中则被称为「解释」，被处理成模型里的一个给定函数. 然而，这种表示关系是需要分析和解释的：从导言中的两个例子就能看出来，学习语言和符号的人不可能单单观察语词和世界就能总结出其间的表示关系. ta们必须观察语言使用者怎么使用这些词——观察由特定规则约束的语言运用. 在晚期维特根斯坦看来，正是这种运用建立并维持了语言和世界之间的表示关系. 一根带有划痕的棍子和测量尺有什么区别？后者之所以是后者，就是因为它被以特定方式运用. 同样，符号或声音的组合也因为被运用而成为语言，这种运用便被称为语言游戏.

Hintikka

Stenius (1967) 根据自己的理解设想了一个简单的语言游戏：假设有个园丁和她的助手，她们负责的花床分成许多小块，每一块上都种了花. 首先，每天和都去检查花床，然后在纸上记录若干符号给检查：, , , , 等等. 这些符号被用来表示开花状况：, , 表示小块的名字，, 表示开花与否. 但这些预期中的意义并不是由直接告知的，只根据花床的实际情况告诉每个记录是对还是错. 当通过这种方式学会了符号的运作后，就不再需要每天去花园了，只需要阅读每天的纸条就能得知花园里的信息. 这便是可以产生意义的语言游戏.

语言游戏不是语言中[13] 的游戏，而是通过语言进行的游戏，往往涉及非语言的语境，比如上文中的开花情况. 而语言片段的意义由其在这种游戏中的角色确定. 语言学习者要确定一个语言片段的意义，只需要观察游戏玩家对其如何反应. 如何验证「房间里有两个球」这句话 [14] ？很简单，到房间里去，看看能不能找到两个球. 可以看到，这种语义学观点引入了行动者，它们通过特定规则的行动来验证句子是否成立. 沿承这一思路，我们便可以发展出博弈语义[15].

[13] 假设我们谈论的语言是汉语，那么汉语同时是元语言和对象语言. 这里的「语言中」可以理解成「在作为对象语言的语言中」. 这样，「『快乐』可以叠词化，但『悲伤』不可以」就是一条词语在「语言中」的运用规则.

[14] 此处有一个问题：在日常语境中说出的「房间里有两个球」这句话，在何种意义上是属于单一语言层次的句子，而非一个宣称「房间里有两个球」这个对象语言句子为真的元语言句子？在语言游戏的理论中，这句话似乎是后者. 在下文对博弈语义的介绍中，我们可以看到，语言使用者自己并不参与语言所代表的博弈，而是对这个博弈的必胜策略作出存在性宣称. 如果该说法成立，那么原文这个问题中的「房间里有两个球」指的是对象语言中的该句子.

[15] 博弈语义多大程度上是维特根斯坦所说的语言游戏？本文第8节有相关讨论.

用游戏解释语言：博弈语义简介（上）哲学第5张一阶逻辑语言的博弈语义

考虑以下句子：

在Tarski语义中，它的意思是「对于每个，都存在，使得等于」. 但是，这看着有点像是逻辑语言句子的字面翻译，我们平时很少会这样说话. 如何用更自然的方式解释句子的意思？日常对话中（或许也不是那么日常，比如在向人解释数学题时）我们也许会说：「不管是多少，都能找到一个和相等的y」. 事实上，有的自然语言中表示「存在」的词组字面意义就是「能找到」(Hintikka & Sandu, 2011). 这便是用博弈来解释语言：「找到」就是玩家的行动（move, 如下棋时的一步棋），而「能找到」就是宣称「玩家存在达到某一目标的策略」（如象棋中宣称「某个马能跳到某处」）. 目标是什么？就是让成立. 在解释这个句子时，我们已经不自觉地代入了博弈中一个玩家的身份. 为表述便利，把我们代入的玩家称为Myself. 因为是我们的目标，所以可以将其看作是博弈中Myself胜利的条件：如果最后的结果是等式成立，那么Myself赢，否则输.

只有一个玩家是不构成博弈的. 另一个玩家呢？再想想句子的解释：不管是多少，都能找到一个和相等的. 当这场博弈轮到Myself作出选择时，已被选好了，且这一选择不受Myself控制，Myself的选择是建立在一个给定的的基础上的——这便是另一个玩家的选择.将其称为Nature.

至此，我们将句子转化成了一场回合制博弈. 这场博弈有两个玩家，博弈流程是首先Nature选择一个对象代入，然后Myself选择一个对象代入. 如果，那么Myself赢，否则Nature赢. 何时为真？当且仅当Myself有必胜策略，此时不管Nature选择了什么样的值代入，Myself都总能依据必胜策略找到一个相等的值代入，赢得博弈. 容易看出，句子的博弈语义「Myself在代表的博弈中有必胜策略」和的Tarski语义「对于每个，都存在，使得」是等价的（即真值相同），读者可自行验证.

将上面的例子一般化：在博弈语义中，每个句子都被看成一个双玩家博弈. 在第一节中提到过，句子的语义和真值离不开具体模型，所以，更准确地说，每个句子在一个给定模型中都被看成一个双玩家博弈，将其称为（在模型不重要或者可以通过上下文确定时，也可以直接记为). 有了，如何确定的真假？在中为真（记作），当且仅当Myself在中有必胜策略；在中为假（记作）[16]，当且仅当Nature有必胜策略[17]. 那么，又要如何确定一场博弈的输赢？回想我们如何确定一场井字棋的输赢：首先，我们需要知道赢棋的定义，也就是说在所有终局里，哪些局面算先手赢，哪些局面算后手赢；其次，对于并非终局的局面（比如博弈刚开始的空棋盘），我们需要知道有哪些博弈规则，也就是要知道棋要怎么下、怎么走到终局. 对于井字棋，这样的博弈规则很简单：双方轮流下子、必须选择九个位置中没有棋子的空位下. 对于其它很多博弈（如象棋），规则就要复杂很多.

[16] 注意，这里不像第一节的Tarski语义一样记作，因为后者是「非真」的意思，但下文将介绍一种并非非真即假的语言，「非真」和「假」是不同的概念. 当然，FOL的句子在博弈语义中仍然是非真即假的，但这需要另外证明.

[17] 这自然提供了从一阶逻辑语言到存在二阶逻辑语言 (existential second-order logic) 的翻译：只需要在后者中直接声称前者中的句子所代表的博弈存在一个必胜的策略函数即可.

要确定句子代表的博弈的输赢也是一样，需要确定终局输赢规则和非终局博弈规则. 对前者，回想我们确定句子代表的博弈终局输赢的方式：如果，那么Myself赢，否则Nature赢. 将其一般化，在中，终局就是是原子公式的局面，此时已经不能再作有意义的拆分，博弈也就没有下一步可走. 自然，如果这个原子公式成立，那么Myself赢，否则Nature赢，至于这里「成立」的标准不定，为方便起见可以照搬Tarski语义里的定义 [18]. 将这条规则形式化为：

[18] 我们给出的博弈语义只用来解释连结词和量词，将原子命题的真假视为给定的.

(1, 暂定) 当博弈进行到且为原子命题时，按照Tarski语义同样的方式判定真假. 若在中为真，则Myself赢，否则Nature赢.

这并不是准确的定义，马上会被修正. 但至少我们暂时有了一个终局输赢规则，至于非终局博弈规则，句子为我们提供了量词和的例子. 将相应的规则形式化为：

(2，暂定) 当博弈进行到时，这一回合由Myself从的论域中选择一个对象代入. 博弈继续，假设所选的对象在目标语言中名为c [19]，则下一回合的博弈局面为.
(3，暂定) 当博弈进行到时，这一回合由Nature行动，规则其余部分同(2，暂定).

[19] 这要求对于每个论语中的个体，目标语言中都有相应的名字. 我们假设其成立.

其它的情形呢？先考虑. 这个句子成立，当且仅当和中存在一个成立——和起着类似的作用，都刻画某种存在性. 因此，自然应该是Myself的回合，则相反：

(4，暂定) 当博弈进行到时，这一回合由Myself从和中选择一个. 博弈继续，假设所选的数为，则下一回合的博弈局面为.
(5，暂定) 当博弈进行到时，这一回合由Nature行动，规则其余部分同(4，暂定).

至于，其作用是颠倒句子的真值，而博弈语义中真值是由玩家是否存在必胜策略确定的：一方面，为真为假Nature在中有必胜策略；另一方面，为真Myself在中有必胜策略，也就是说Nature在中有必胜策略Myself在中有必胜策略，玩家名调换同样成立. 考虑下面这个句子：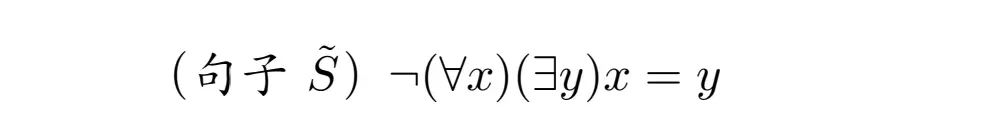

用游戏解释语言：博弈语义简介（上）哲学第7张

即是在最前面加上所得的句子. 设想将通过某种方式去掉后，再按照规则把其中的量词分别除去（假设分别用和代入了和），来到终局，只剩下最后的原子命题时，我们会发现，根据上一段的讨论，如果为真应该是Nature赢，为假则应该Myself赢，但这和(1, 暂定)给出的定义相反. 可以说，起到了颠倒玩家角色的作用. 我们为此引入「角色」的概念：将Nature本来的角色称作证伪者 (falsifier), Myself本来的角色称作证实者 (verifier)，将 (1, 暂定) 中的输赢定义修改为原子命题成立则证实者赢（此时证实者可能是玩家Myself，也可能是玩家Nature），否则证伪者赢，其它条目也相应修正. 于是：

(6) 当博弈进行到时，两个玩家的角色颠倒. 博弈继续，下一回合的博弈局面为.
(1, 修正) 当博弈进行到且为原子命题时，按照Tarski语义同样的方式判定真假. 若在中为真，则此时角色为证实者的玩家赢，否则此时角色为证伪者的玩家赢.
(2，修正) 当博弈进行到时，这一回合由证实者从的论域中选择一个对象代入. 博弈继续，假设所选的对象在目标语言中名为，则下一回合的博弈局面为.
(3，修正) 当博弈进行到时，这一回合由证伪者行动，规则其余部分同(2，修正).
(4，修正) 当博弈进行到时，这一回合由证实者从和中选择一个. 博弈继续，假设所选的数为，则下一回合的博弈局面为.
(5，修正) 当博弈进行到时，这一回合由证伪者行动，规则其余部分同(4，修正）.

至此，我们给出了FOL全部的博弈语义[20]. 在假设选择公理 [21] 成立的前提下，可以证明，对于FOL而言，博弈语义与Tarski语义等价，也就是说，在同一个模型下，一个FOL句子在博弈语义中为真，当且仅当其在Tarski语义中为真. 我们可以用一些简单的句子验证这个结论：考虑, 它对应的博弈是这样的：初始局面下Myself为证实者，Nature为证伪者，第一个使得双方角色对调，接着由此时的证实者，也就是Nature任意选取一个个体代入，然后双方角色再对调，如果成立那么此时的证实者也就是Myself赢，否则Nature赢. 不难看出这个博弈的输赢条件和是一模一样的，因此这两个句子在博弈语义中等价——这也正是Tarski语义给出的判断.

[20] 读者可能发现我们没有给出的博弈规则. 这并不是必要的，因为任何一个包含的FOL句子都能被改写成等价的不含的形式：. 对于对此心有不安的读者，也可以用子博弈的概念给出的博弈规则，见Hintikka & Sandu (2011), Section 8.2.6

[21] 集合论的ZFC公理系统中的一条公理，数学家对其使用有所保留.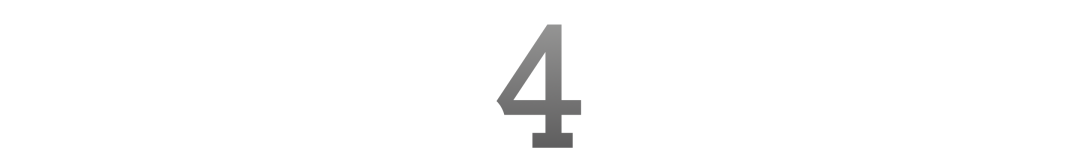

用游戏解释语言：博弈语义简介（上）哲学第8张 IF-逻辑及其博弈语义

为什么需要博弈语义？在第二节中我们简单介绍了语言哲学层面的一些考量. 但除此之外，无论是用于解释逻辑语言还是自然语言，博弈语义的效力都有胜过Tarski语义之处，能够解释一些后者难以解释的语言现象. 本节将首先介绍FOL中的一条隐藏假设，然后指出这条假设并非必要，并在FOL的基础上构造一种不需要该假设的表达力更强的逻辑语言，最后说明相较Tarski语义，博弈语义解释这种语言更为便利.

考虑以下两个FOL中的句子：

它们的意义是否相同 [22]？不论用哪种语义解读，都很快能发现答案为否. 事实上为真时不一定为真：在所有模型中都为真 [23]，而仅在论域里只有一个个体的模型中为真（假设论域里不止一个个体，那么不管用哪个个体代入, 都能在论域中找到和不同的另一个个体，因此找不到满足的). 例如，如果论域是实数集，那么在博弈语义下，说的就是「不管是多少，都能找到一个和相等的数」（显然，这个数就是自身），而说的则是「能找到一个数，它和所有数都相等」. 这两个陈述的意义不同，一眼便知.

[22] 什么叫意义相同？我们可以用逻辑等价来刻画这个概念. 两个逻辑语言中的句子与等价，当且仅当两个句子为真的条件相同，即为真为真. 具体来说，.

[23] 一般我们规定模型的论域为非空集. 如果论域为空集，那么此时S 为假.

从上例中可以看出，FOL中量词的先后顺序可以改变句子的意义. 为什么会这样？这显示出了FOL中的一条隐藏假设：对于形如的公式，各个量词并不是简单并列的，而存在一定的结构，大致来说，后面的（里面的）量词依赖于前面的（外面的）量词. 在中，在的辖域内，所以受到前者约束. 这用博弈语义很好解释：在解读时，首先由Nature选择一个个体代入, 然后由Myself选择一个个体代入, 并且因为Myself的选择发生在后，假定其能「看到」Nature先前的选择，这样Myself就可以据此来选择不同的个体代入. 例如，在用实数集解读的情形中，唯有预设了「能看到」的假定，才能保证代入后成立：如果Nature选择了2, Myself才得以也选择2; 如果Nature选择了, Myself才得以也选择（看到先前的选择后能不能将其忽视？当然可以，即使Myself看到了Nature的选择，Myself的选择也完全可以不依赖于Nature的选择. 但由于决定句子真假的不是单次博弈的胜负，而是「有没有必胜策略」，重要的是Myself的选择是否能够依赖于Nature的选择，这在Myself不知道后者的情况下显然是不可能的）. 而在中，Nature是先选择的一个，在其选择时没有任何可以参考的信息，因此只能随意选择一个确定的个体代入（我们不考虑投骰子决定选择哪个个体这类情况）. 相反，Myself可以根据Nature的选择决定自己要选择哪个个体代入. 两个博弈中玩家对信息的掌握情况不同，因此两个句子显然是有区别的.

但FOL的这条假设一定要成立吗？落在其它量词辖域内的量词一定要依赖于外层量词吗？呜呼，就像欧几里得第五公设一样，它看起来并没有什么很好的理由，完全可以放弃. Hintikka & Sandu (2011) 直言不讳地将其称为弗雷格和罗素（在设计现代的逻辑语言时）犯下的错误. 嵌套量词间的独立是完全可以设想的，事实上我们也的确能遇到这样的例子. 学过数学分析或者高等数学的读者应当知道函数的连续性与一致连续性的经典定义. 函数在满足以下条件时被称为连续的：对所有和所有，都存在满足以下条件：对所有, 如果, 那么. 而如果把以上定义中的「都存在」改为「都存在依赖于但不依赖于的」，那得到的就是对一致连续性的定义. 这里，就独立于.

自然语言中也有这样的例子，如 "Some friend of each townsman and some neighbour of each villager envy each other"就无法翻译成FOL句子. 注意，"some neighbour" 是独立于 "each townsman" 的，如果直接翻译成的形式，会依赖于, 也就是说，在逐一检查friend of townsman和neighbour of villager之间的关系来核验这句话时，即使考察同一个villager, 不同的townsman也可能对应到不同的neighbour of villager, 这显然并非原句所想表达的.

从上面的例子中可以看出，FOL因为假设了嵌套量词间的依赖性，表达力受到了限制，无法描述这种量词间的独立关系. 为此，我们在FOL的基础上定义一套新的逻辑语言，称为IF-逻辑 (independence-friendly logic，或称information-friendly logic，下文简称IFL) [24]. 相较FOL，其增加了两类新的量词：和, 它们表示「/」前的量词与「/」后的量词独立. 相应地，IFL公式相比FOL有一些扩充：

[24] 与FOL的情形相似，IFL也可以有不同的版本，对FOL进行不同扩充，本文为便利起见，选择了最简单的一种扩充方式.

定义3（IFL公式）：
(1) 所有FOL公式都是IFL公式.
(2) 如果在一个IFL公式中有一个落在的辖域中，那么将其替换为，得到的也是IFL公式.
(3) 如果在一个IFL公式中有一个落在的辖域中，那么将其替换为，得到的也是IFL公式.

IFL的句法已经建造好了，要如何解读呢？Tarski语义在这里遇到了麻烦. 考虑这个句子：

我们会发现，没有办法像FOL的Tarski语义那样逐个把量词拿掉，因为无论以怎样的顺序处理，都总会至少有一个存在量词依赖于两个全称量词 [25]. 这时博弈语义便显得十分自然：对句子, 我们说过，因为发生在之后，我们假定Myself在选择时能看到Nature作出的选择，这样才可能依赖于. 如果要刻画量词独立的情况，那只要简单去掉这一假定即可——只要当Myself选择时不知道Nature作出的选择，那么其选择就不可能依赖于Nature的选择，因而是独立的. 因为这种独立本质上是玩家所知道的信息之间的独立，我们将其称为信息独立.

[25] Tarski语义并非完全不能解读量词独立句，逻辑学家们早已提出了各种解决方案，如将文中IFL句子中的看作单个量词（称为广义量词或Henkin量词）. 但这些解决方式不如博弈语义自然，并且在解读自然语言时会出现问题，不能和自然语言的句法对应.

如何表示「Myself选择时不知道Nature此前作出的选择」呢？简单的回答是，将Nature的选择从Myself策略函数的论元中去掉. 在此，我们首先用少量篇幅为不熟悉博弈论的读者介绍博弈论中如何刻画玩家对信息的掌握. 以信息流动为标准，博弈可以分为两种类型. 在象棋这样的博弈中，所有玩家在所有博弈阶段都知道博弈中此前发生的所有事件（包括初始事件，即各玩家的初始局面），这类博弈称为完美信息博弈. 与此相对，在不完美信息博弈中，并非所有玩家都知道所有信息，比如在绝大多数牌类游戏中，通常各玩家的手牌只对自己或某些特定玩家展示. 显然，FOL句子所代表的博弈属于前者，而IFL则属于后者.

接下来，我们对「必胜策略」这一概念给出更严格的刻画，并用其描述玩家对信息的知识. 什么是策略？在博弈论中，一个玩家的策略通常被定义为一个函数，对于每个轮到该玩家行动时可能出现的博弈局面，策略函数输出该玩家的一个选择. 必胜策略的定义则正如其字面意义：如果某玩家按照某策略行动一定能赢，那该策略就是该玩家的一个必胜策略. 在FOL句子所代表的博弈中，由于双方都知道对方之前的选择，每一步可以据此来行动，因此「轮到该玩家行动时可能出现的博弈局面」可以由另一玩家此前作出过的所有选择唯一决定. 以句子: 为例，双方的策略函数输入博弈局面，输出一个论域中的个体以供玩家代入进变量. 该博弈中双方各只有一个回合. 在Nature的回合中，由于第一个回合没有任何信息可供参考，Nature的策略函数输入固定的空白初始局面，因此输出的也是一个固定值. 但由于Myself不知道Nature的策略（即使在完美信息博弈中，玩家也完全可以不知道彼此的策略！策略是在玩家脑子里不可见的选择，和可见的行动不同），Myself的策略函数将输入此时的局面（即Nature的选择），输出一个论域中的个体. 这样，以Myself的视角观之，在其选定了一个策略后整场博弈的走向就由Nature决定，Myself的行动只是以固定的方式回应Nature的行动而已. 例如，考虑以下句子：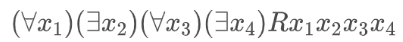

用游戏解释语言：博弈语义简介（上）哲学第10张

记Myself的策略函数为, 记Nature在两个回合中选择的个体为, , 则博弈结束时的局面可以被记为, Myself的选择完全依赖于Nature的选择. 敏感的读者可能会问：怎么时而是一元函数，时而是二元函数？这只是我们为方便采取的写法. 事实上的论元应当是博弈局面，但由于博弈局面可以完全被Nature的选择唯一决定，因此我们直接将, 放在论元的位置.

经过上面的介绍，坚持阅读到这里的读者想必可以回答上文未解决的问题了：如何在博弈语义中表示「Myself选择时不知道Nature作出的选择」？很简单，把Nature的选择从Myself此时的策略函数的论元中去掉就可以了. 这就已经给出了IFL与FOL博弈语义的全部不同之处. 事实上，如果读者尝试自己为IFL给出像上节那样的博弈规则，会发现独立版本的量词的博弈规则和对应的FOL量词一模一样，这是因为信息独立并不发生在博弈规则层面，而发生在策略层面: 当且仅当Myself有满足如下条件的必胜策略：当进行到时，Myself的策略函数论元中不包括Nature在相应回合的选择，如此等等.

回顾上节介绍的博弈规则可知，玩家在博弈进行到连结词和量词这两类情况时会采取行动. 既然博弈语义将量词独立解释为玩家对彼此行动的信息不对称，那其他涉及玩家行动的信息独立便也很好设想了：除了这类信息独立，自然还可以有, 与三类，甚至还可以有和等，表示在相应的回合中玩家无视之前某个造成的角色交换. 后文将会引入更多博弈规则，它们之间都可以有信息依赖/独立两种情况. 这些独立版本的逻辑语言可以统称为IFL，语法与语义定义可以参照上文给出，在此不再赘述，下文将直接使用.

用游戏解释语言：博弈语义简介（上）哲学第11张 IF-逻辑和博弈语义的一些特点

我们下文（第6节）将指出，IF-逻辑比一阶逻辑更适合用来表示自然语言的逻辑形式（logical form）. 如果这个观点成立，那么从本节中所介绍的IF-逻辑的特点中可以推论出自然语言（的博弈语义）的一些有趣性质.

表达力强于FOL

由于所有FOL句子都是IFL句子，而许多IFL句子则不能找到等价的FOL翻译，我们可以说，IFL的表达力强于FOL. 什么是表达力？对于一种逻辑而言，表达力就是其区分不同模型的能力：对于两个模型和，如果一种逻辑中能找到句子使得在这两个模型中的真值不同，我们就说能区分和. 当我们说FOL可以表达某个概念，比如等价关系时，我们的意思是，对于任意一个二元关系符号，都存在一组FOL句子，这组句子在一个模型中为真当且仅当在其中被解释为一个等价关系. 在这个定义下，FOL不能表达但IFL能表达的概念有：戴德金无穷、非完全线性序、不连通图、一阶逻辑公式外延等势、开集，等等.

并非非真即假

我们说过，可以想见，博弈中并不一定存在任何玩家的必胜策略: 一方面，不一定所有终局都是你死我活的，如果有一部分终局被定义为平局，那显然有可能所有玩家都没有必胜策略（如所有终局都是平局时）. 另一方面，即使所有终局都有确定的赢家，必胜策略也可能对于所有玩家都不存在. 比如，即使在猜拳游戏中规定原本的平局全都算作某玩家赢，双方也还是都没有必胜策略. 有玩家有必胜策略的博弈称为决定博弈 (determined game). 回想博弈语义中对句子真值的定义：如果Myself有必胜策略则句子为真，如果Nature有必胜策略则句子为假. 自然，如果句子代表的博弈是决定博弈，那么句子非真即假. 但如果不是呢？

可以证明，IFL便是不满足非真即假的逻辑语言. 考虑下面这个简单的例子：. 两个玩家都需要在什么信息都不知道的情况下各选择一个个体，这两个个体如果一样则Myself赢，不一样则Nature赢. 容易看出，在任何一个论域中至少有两个个体的模型中，两个玩家都没有必胜策略，输赢完全是概率问题. 因此，在中，这句话既非真又非假，处在真值的间隙中.

这使得IFL有一些不同于FOL的有趣性质. 例如，IFL显然不满足排中律（对于任意句子,和任意模型, ). 不过排中律的爱好者不必过于沮丧，我们当然可以定义另一种更弱的否定（用表示），使得, 显然这种否定是满足排中律的（思考：自然语言中的否定是哪种？）. 此外，在FOL中可以直接将两个句子和的等价定义为, 而IFL中需要如此定义：和真值等价(truth equivalent)，当且仅当; 它们假值等价(falsity equivalent) ，当且仅当; 它们逻辑等价 (logically equivalent) ，当且仅当它们真值等价且假值等价. 最后，在考虑句子为真的条件时，由于需要确定的是Myself的必胜策略，因此和这样的对Nature策略的限制就成了无效限制，反之，考虑句子为假的条件时，对Myself策略的限制是无效的 [26]. 考虑下面这个句子：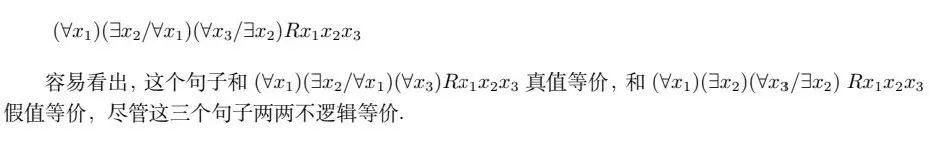

用游戏解释语言：博弈语义简介（上）哲学第12张

[26] 当然，这里说的是初始角色下的情况.

非组合性

这一性质是关于博弈语义而非IF-逻辑的. 组合性 (compositionality) 通常被表述为：一个复杂语言片段的意义由其组分的意义和组分之间的结合方式确定. Tarski语义显然满足于这一条件：比如，要确定的意义，必须先确定和的意义，然后通过它们的组合方式计算出整个片段的意义. 可以说，组合性要求语言片段的意义从内而外被构造出来. 然而博弈语义是从外而内解读的语义，的意义（是否有Myself的必胜策略）并不来自或（这两个句子是否有Myself的必胜策略）.

Hintikka

因此，博弈语义是非组合的——尽管它可能和别的组合性语义等价. 在FOL中情况显然如此，至于IFL, 也早已有人给出了组合性语义. 因此，对我们讨论的逻辑语言来说，博弈语义是否满足组合性似乎并不重要. 但对自然语言而言，非组合语义在解读句子时不必严格遵守句法的结构限制，因此更为自由，有时能使语义理论免去一些额外的假设，更为简洁（见第7节回指代词部分）.

除此之外，IF-逻辑还有一些有趣的性质，比如并非递归可公理化 (recursively axiomatisable). 如果自然语言需要用IFL刻画，这将导致没有有效算法能判断一个自然语言句子是否是分析命题，或两个句子是否同义. /

用游戏解释语言：博弈语义简介（上）哲学第14张点亮「在看」，让更多人看到

本篇文章来源于微信公众号: Philosophia 哲学社

推荐阅读：
游子带你看世界｜老团员采访之Cindy
游子|我们为何一次又一次地选择回来？
翻译经验+爱心捐助，为什么不能在一起呢？

版权声明：“备战深国交网”除发布相关深国交原创文章内容外，致力于分享国际生优秀学习干货文章。如涉及版权问题，敬请原作者原谅，并联系微信547840900（备战深国交）进行处理。另外，备考深国交，了解深国交及计划参与深国交项目合作均可添加QQ/微信：547840900（加好友时请标明身份否则极有可能加不上），转载请保留出处和链接！
非常欢迎品牌的推广以及战略合作，请将您的合作方案发邮件至v@scieok.cn

本文链接：http://shenguojiao.scieok.cn/post/4007.html

分享按钮

哲学微信公众号：scieok
微信号：ScieOk_cn

加微信，发送 2021 即可进群获取深国交备考资料，并有定期分享相关教育心得